Los Cuadriláteros

Son cuadriláteros todos los polígonos delimitados por cuatro lados; y que en consecuencia contienen cuatro ángulos, con sus respectivos vértices.

---

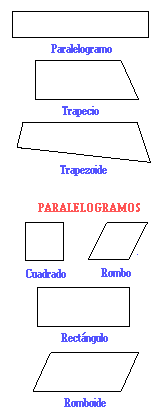
Clases de cuadriláteros.

Los cuadriláteros se clasifican en consideración a la posición que ocupan sus lados, en: Paralelogramos — cuando los dos pares de sus lados son paralelos entre sí. Trapecios — cuando solamente dos de sus lados son paralelos entre sí. Trapezoides — cuando ninguno de sus lados es paralelo a otro. Los paralelogramos son: El cuadrado — cuyos cuatro lados son iguales y sus cuatro ángulos son rectos. El rectángulo — que tiene iguales dos lados, y los otros dos distintos pero iguales entre ellos (por lo cual es usual decir que son iguales dos a dos) y cuyos cuatro ángulos son rectos. El rombo — cuyos cuatro lados son iguales pero tiene dos ángulos agudos iguales y dos ángulos obtusos iguales. El romboide — que tiene sus lados iguales dos a dos, pero tiene dos ángulos agudos iguales y dos ángulos obtusos iguales.

---

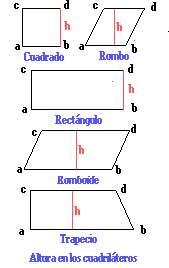
Altura de los cuadriláteros.

La altura de los paralelogramos, se determina indistintamente tomando como base cualquiera de sus lados, y consiste en la distancia perpendicular entre la base, y el lado opuesto. Naturalmente, en el cuadrado la altura siempre será equivalente al lado, por ser todos iguales. En el rectángulo, cuando el lado menor sea la base la altura será el lado mayor; y viceversa. En el rombo, el romboide y el trapecio, la altura será la distancia perpendicular entre los lados paralelos.

---

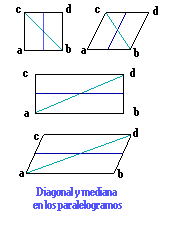
Diagonal y mediana de los cuadriláteros.

En los cuadriláteros, se denomina diagonal a una línea que une dos ángulos o vértices opuestos. En los cuadriláteros, se denomina mediana a una línea que une los puntos medios de dos lados opuestos.

---

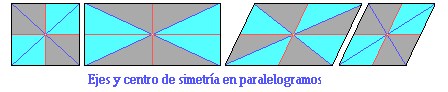
La simetría.

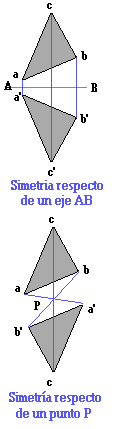La palabra simetría hace referencia a una igualdad de medidas a través de una línea llamada eje de simetría; y se aplica a la cualidad de aquellas figuras planas que son iguales aunque se presentan en una posición distinta respecto de una línea (como en una imagen de espejo). Además existe simetría en otras formas; que pueden ser no a través de una línea sino de un punto, en cuyo caso se trata de un punto de simetría; y no necesariamente de figuras geométricas sino en relación a cualquier imagen plana. Una misma figura, en algunos casos, puede tener simetría a la vez respecto de un eje y respecto de un punto, que en ciertos casos constituye su centro de simetría Los paralelogramos se caracterizan porque tienen la propiedad de generar nuevas figuras exactamente iguales, cuando se dividen mediante una diagonal o una mediana; por lo cual tienen a la vez eje de simetría y centro de simetría.

---

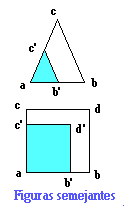
Igualdad y semejanza en las figuras geométricas.

Dos figuras geométricas son iguales cuando tienen iguales todos sus lados y todos sus ángulos; y por lo tanto tienen la misma forma y el mismo tamaño. Dos figuras geométricas son semejantes cuando tienen iguales sus ángulos, pero sus lados son diferentes; y por lo tanto tienen la misma forma y distinto tamaño.